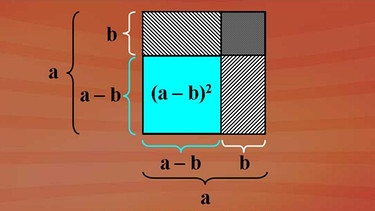
Um eine weitere binomische Formel herleiten zu können, wollen wir unsere ursprüngliche quadratische Fläche mit der Seitenlänge a nicht wie vorher um b Längeneinheiten vergrößern, sondern verkleinern.

Kürzen der Längeneinheiten

Kürzen der Längeneinheiten - klicken Sie bitte auf die Lupe

Das Anfangsquadrat mit der Seitenlänge a wird verändert, indem die Seitenlängen a jeweils um b Längeneinheiten verkürzt werden. Es ergibt sich ein kleines Quadrat mit der Fläche a minus b mal a minus b. Wie können wir jetzt diese Fläche ohne Produktschreibweise, nämlich in der Summenschreibweise darstellen? Dazu gehen wir von der ursprünglichen Quadratfläche a² aus und versuchen die Veränderungen der Fläche nach und nach zu ermitteln.

Durch die Verkürzung um b Längeneinheiten werden zwei Teilflächen a mal b gebildet, die wir von der Gesamtfläche subtrahieren. Wir erkennen aber, dass das Quadrat mit der Seitenlänge b einmal zu viel subtrahiert wurde. Um diesen Fehler auszugleichen, addieren wir die Fläche des Quadrates mit der Seitenlänge b einfach wieder dazu. Damit haben wir die Fläche in der Summenschreibweise.

Ausmultiplizieren von Klammern

Natürlich hätten wir diese beiden Formeln auch über das Ausmultiplizieren von Klammern erhalten können:

Ausmultiplizieren von Klammern

Die beiden Klammern a minus b nach der Regel jedes Glied der ersten Klammer mit jedem Glied der zweiten Klammer multipliziert ergibt a mal a gleich a² , dann plus mal minus gibt minus a mal b, minus mal plus gibt minus b mal a, wofür man aber auch a mal b schreiben darf, da Faktoren vertauscht werden dürfen, und zum Schluss noch minus mal minus gibt plus und b mal b gibt b². Die a und b-Glieder können wir nun zusammenfassen zu minus 2 mal a mal b und die beiden äußeren Terme schreiben wir ab.

Dritte binomische Formel über das Ausmultiplizieren von Summen

Wir wählen das Produkt aus der Summe und der Differenz zweier gleicher Terme. Und für die gleichen Terme, wie bisher, die Platzhalter a und b.

Ausmultiplizieren von Klammern - klicken Sie bitte auf die Lupe

a plus b in Klammern mal a minus b in Klammern gibt dann a mal a mit a², für plus a mal minus b minus ab, für plus b mal plus a plus b mal a oder auch ab geschrieben und plus b mal minus b gleich minus b². Minus ab und plus ab heben sich auf und es bleibt a² minus b².

Als Formel geschrieben, a plus b in Klammern mal a minus b in Klammern in der Produktschreibweise ist a² minus b² in der Summenschreibweise.

Grafische Darstellung

Grafische Darstellung - klicken Sie bitte auf die Lupe

Die Ausgangsfläche a mal a gleich a² ist uns bereits bekannt. Wir verkürzen nun eine Seite um b und verlängern gleichzeitig die andere Seite um die gleiche Seitenlänge b. Die Fläche des neu entstandenen Rechtecks, es ist diesmal kein Quadrat, beträgt somit Seite a plus b mal Seite a minus b. Von unserem Ausgangsquadrat mit der Fläche a² muss das Rechteck mit den Seitenlängen a und b, demnach der Fläche a mal b subtrahiert werden. Jetzt fehlt aber rechts unten ein Flächenstück. Deshalb addieren wir die Rechtecksfläche a mal b. Aber aufgepasst, plötzlich ergibt sich rechts oben eine quadratische Fläche mit der Seitenlänge b zu viel. Um dies wieder auszugleichen subtrahieren wir ganz einfach dieses Flächenstück b². Und siehe da, die beiden Terme minus a mal b und plus a mal b heben sich auf und es bleibt a² minus b² übrig.

Zusammenfassung

Tabellarische Darstellung - klicken Sie bitte auf die Lupe

Wir haben von der Produktform, der Quadratform und der Summenform als Schreibweisen gesprochen. Bezeichnet haben wir die Formeln als 1., 2. und 3. Binom. Tragen wir unsere nachgewiesenen Formeln ein, ergibt sich die gezeigte tabellarische Darstellung für unsere drei binomischen Formeln.