Zeit-Höhenmeter-Diagramm

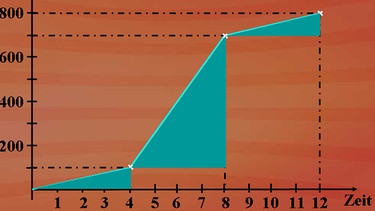
Beginnen wir zur Veranschaulichung mit diesem Beispiel: In Lenggries führt eine Seilbahn zur 1.500 Meter hoch gelegenen Bergstation. Sie überwindet dabei in zwölf Minuten Fahrzeit einen Höhenunterschied von 800 Metern. Wie sieht die grafische Darstellung in einem Zeit-Höhenmeter-Diagramm aus? Klicken Sie auf nebenstehende Grafik: Das Bild lässt erkennen, dass es sich wohl um unterschiedliche Steigungen handeln muss.

Erstes Merkmal: die Steigung

Damit sind wir bei dem ersten Merkmal einer linearen Funktion: die Steigung. Unsere Grafik besteht aus drei Teilbereichen mit unterschiedlicher Steigung. In den ersten vier Minuten eine relativ geringe Steigung, in den nächsten vier Minuten eine starke Steigung und im Schlussbereich wiederum eine geringe Steigung.

Dargestellt sind die Steigungen in Steigungsdreiecken. Die Gerade des Teilbereiches 1 verläuft durch den Koordinatenursprung, die beiden anderen schneiden die y-Achse (hier Höhenmeterachse) unterhalb beziehungsweise oberhalb des Nullpunktes.

Zweites Merkmal: der y-Achsenabschnitt

Damit haben wir das zweite Merkmal einer jeden linearen Funktion: der sogenannte y-Achsenabschnitt. Alle gewonnenen Einsichten werden wir jetzt an Beispielen ausprobieren.

Beispiel 1

Zeit-Höhenmeter-Diagramm

Die Funktionsgleichung y ist ein halb mal x plus 0. Zwei Punkte legen eine Gerade fest. Für x Null eingesetzt, erhalten wir y gleich Null, den ersten Punkt unserer Geraden. Für x gleich zwei eingesetzt, erhalten wir y gleich eins, den zweiten Punkt der Geraden.

Die Null in der Funktionsgleichung zeigt, dass es sich um eine Gerade durch den Koordinatenursprung handelt. Das Steigungsdreieck verläuft mit zwei Einheiten nach rechts in x-Achsenrichtung und einer Einheit nach oben in y-Achsenrichtung. Es kann an jeder beliebigen Stelle der Geraden angesetzt werden. Mit dem Wissen, dass es sich um eine Ursprungsgerade handelt und die Steigung mittels dem Steigungsdreieck eingezeichnet werden kann, ist es uns möglich ohne Berechnung von Punkten die Gerade zu zeichnen.

Beispiel 2

Nun soll im Funktionsterm hinter dem x nicht plus Null sondern minus vier stehen.

Die Funktionsgleichung lautet dann "y gleich einhalbmal x minus vier". Wie vorher für x Null eingesetzt - erhalten wir jetzt aber y gleich einhalbmal 0 minus vier ist minus vier. Und für x zwei eingesetzt: y gleich einhalbmal zwei minus vier ist minus drei. Somit haben wir wieder zwei Punkte, die eine Gerade festlegen. Die Gerade verläuft also parallel zur ersten Geraden, schneidet aber die y-Achse im Punkt Null und minus vier. Diese minus vier kann man wie die Steigung direkt an der Funktionsgleichung ablesen.

Beispiel 3

Beispiel 3

Damit Ihnen das alles noch verständlicher vorkommt, zeichnen wir eine Reihe von weiteren Geraden miteinander ein. Wir bleiben dabei bei Geraden mit der Steigung ein halb. Neben den bereits vorhandenen Geraden "y ist einhalbmal x plus Null" und "y ist einhalbmal x minus vier" noch die Geraden "y ist einhalbmal x plus drei" und "y ist einhalbmal x minus zwei".